Hat Matrix Multiple Regression

It describes the influence each response value has on each fitted value. We call it as the Ordinary Least Squared OLS estimator. In statistics the projection matrix sometimes also called the influence matrix or hat matrix maps the vector of response values dependent variable values to the vector of fitted values or predicted values.

waynes world baby hat weird hat types unique hat storage what does gross mean in german variance of y hat in regression waveshare game hat housing velvet hat box wholesale welches land hat zuerst silvester

Hat Matrix And Leverages In Classical Multiple Regression Cross Validated

5 4 A Matrix Formulation Of The Multiple Regression Model Stat 462

Hat Matrix And Leverages In Classical Multiple Regression Cross Validated

Multiple Linear Regression The Hat Matrix Youtube

Introduction To The Hat Matrix In Regression Youtube

How To Derive Variance Covariance Matrix Of Coefficients In Linear Regression Cross Validated

1A square matrix A is a projection if it is idempotent 2A projection A is orthogonal if it is also symmetric.

Hat matrix multiple regression. Excel worksheet that calculates the coefficients for the multiple regression line using the hat matrix. The Hat Matrix and Regression Diagnostics Paul Johnson October 3 2006 1 OLS Review Myers Montgomery and Vining explain the matrix algebra of OLS with more clarity than any other source Ive found. Was ist wenn wir mehr als zwei Variablen für ein lineares Modell haben.

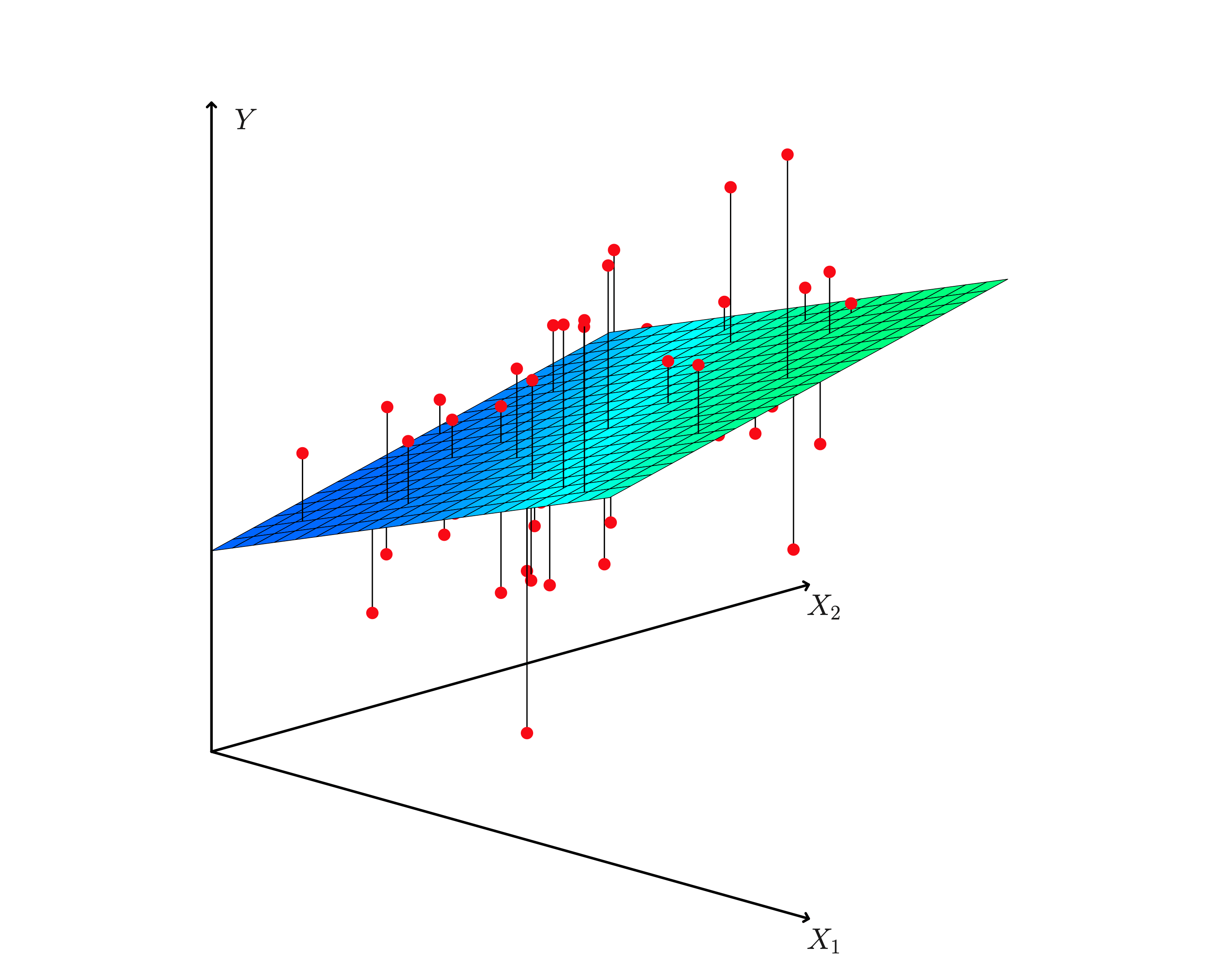
The linearity assumption for multiple linear regression can be restated in matrix terminology as Eε 0 From the independence and homogeneity of variances assumptions we know that the n n covariance matrix can be expressed as Note too that the covariance matrix. These two conditions can be re-stated as follows. Multiple regression modelsthus describe how a single response variableY depends linearly on a number ofpredictor variables.

Matrix notation applies to other regression topics including fitted values residuals sums of squares and inferences about regression parameters. Hat Matrix Y Xb Y XX0X1X0Y Y HY. In this video discuss on Regression Analysis Part 3- Hat Matrix Multiple Linear Regression and this lecture video help for csir net mathematical science.

Frank Wood fwoodstatcolumbiaedu Linear Regression Models Lecture 11 Slide 20 Hat Matrix Puts hat on Y We can also directly express the fitted values in terms of only the X and Y matrices and we can further define H the hat matrix The hat matrix plans an important role in diagnostics for regression analysis. The only criticism I have of their style is that they dont use the hat symbol to dif-ferentiate a parameter estimate from the symbol that represents the true. So far we have seen the concept of simple linear regression where a single predictorvariableXwas used to model the response variableY.

Further Matrix Results for Multiple Linear Regression. Next we will use this framework to do multiple regression where we have more than one explanatory variable ie add another column to the design matrix and additional beta parameters. The Hat Matrix - YouTube.

One important matrix that appears in many formulas is the so-called hat matrix H XXX-1X since it puts the hat on Y. In many applications thereis more than one factor that inﬂuences the response. Multiple Linear Regression.