Y Hat Minus Y Bar
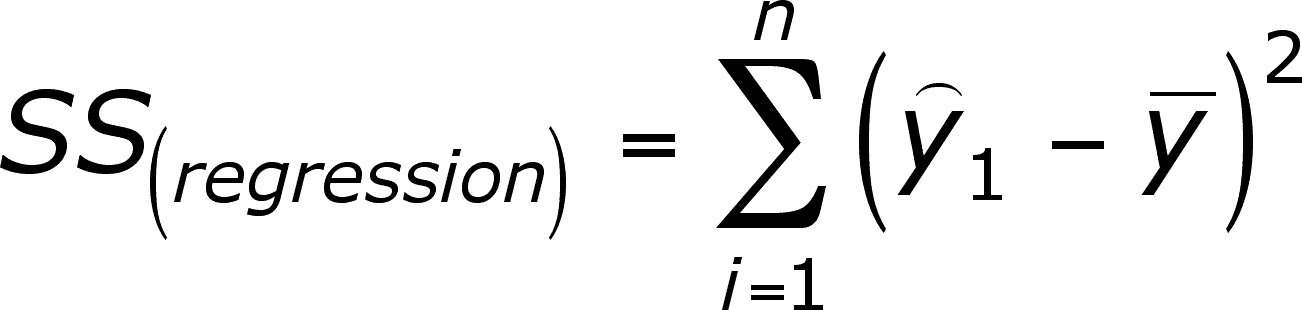
Murray Aug 6 16 at 1452.
Y hat minus y bar. The ordinary least squares estimator for is. In statistics the projection matrix displaystyle sometimes also called the influence matrix or hat matrix displaystyle maps the vector of response values to the vector of fitted values. Thus EY_i - hatY_ihatY_i - barY.
What is the Beta1 hat. If pattern in y why not a pattern in y hat. Defined here in Chapter 3.
Where y is an n 1 vector of dependent variable observations each column of the n k matrix X is a vector of observations on one of the k explanators is a k 1 vector of true coefficients and e is an n 1 vector of the true underlying errors. LlavDem that defines bar to be an infinite loop. Theres no logic for that its just convention.
Consider the standard regression equation Y Xβ ε with predicted value ˆY PXY where PX XX X 1X is the projection onto X or the hat matrix. Intercept symbolized by b-sub-zero equals the mean of the y data points symbolized by y-bar minus the slope symbolized by b-sub-one multiplied by the mean of the x data points symbolized by x-bar. Thus inside the first summation I can replace the sum with k j.
If its talking about quadrant coordinates the Y bar is the vertical center line. The residual plot std res vs the regression fits looks good. Defined here in Chapter 3.
Y-hat is the symbol that represents the predicted equation for a line of best fit in linear regression. So beta 1 is equivalent to adding X in Y minus n of X bars to Y bars by adding X to the square minus n times X to the square which is 07. Jun 3 2015 2.



















